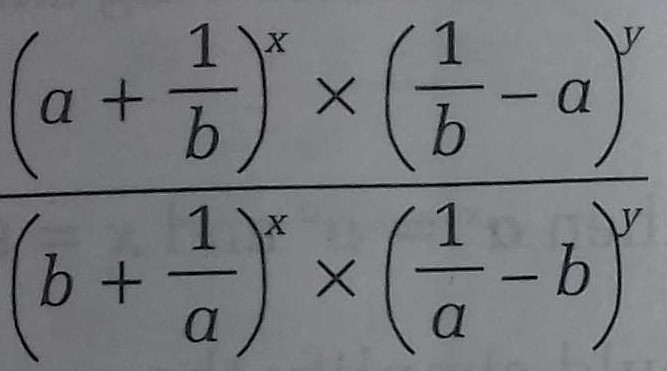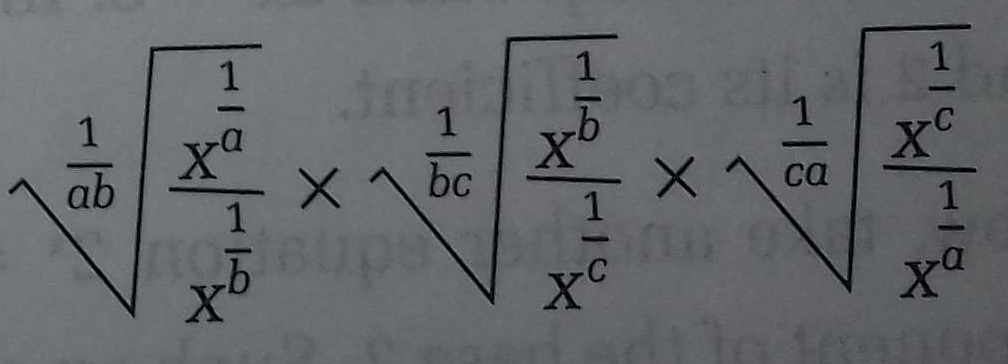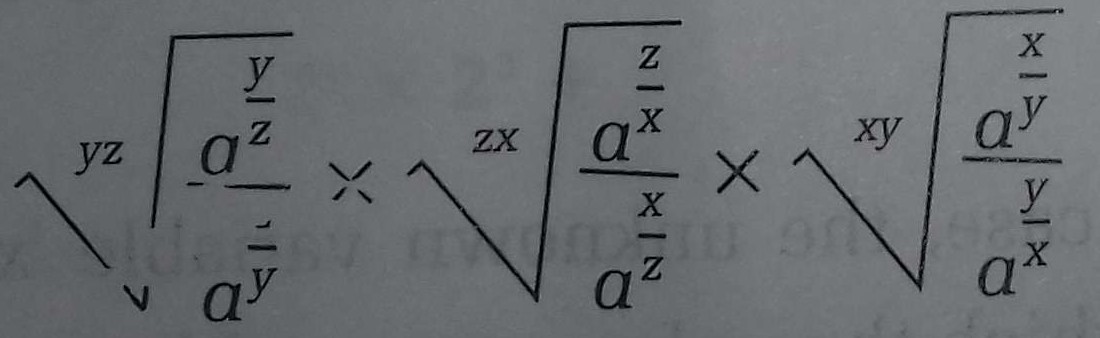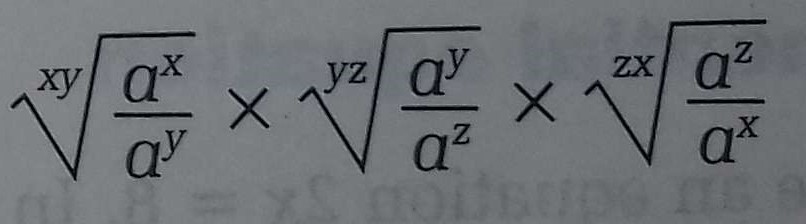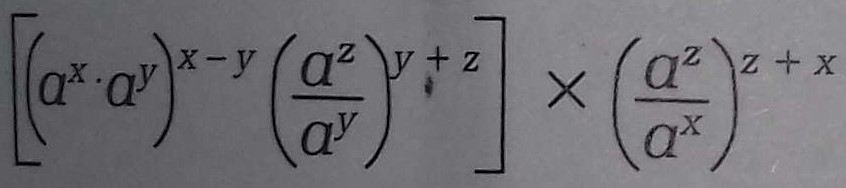Here,       4. 3x+1 - 9x = 27  or, 4. 3x .31 - (3x)2 = 27 Let, 3x .....

Here,        22x - 6.2x+1 + 32 = 0  or, (2x)2 - 6. 2x . 21 + 32 0 Let, 2x .....

Here,       2x-5⨉ 5x-4 = 5 or, (2x / 25) ⨉ (5x / 54) = 5     [ Since, xm .....

Here,        5x-3 ⨉ 32x-8 = 225 or,  (5x / 53) ⨉ (32x / 38) = 225       [ Since, xm - .....

Here,      2x-3 ⨉ 3x-4 = 3-1 or, (2x / 23) ⨉ (3x / 34) = 1/3          [ Since, xm - .....

Here,      2x+3 ⨉ 3x+4 = 18 or, 2x .23 ⨉ (3x .34) =18               [ Since, xm + .....

Here,        5x + 5x + 1 + 5x + 2 = 155 or, 5x + 5x .51 + 5x.52 = 155        [ Since, xm .....

Here,  (√9)x - 3 = (√3)x + 2 or, (3)x - 3 = (3)(x + 2)/2     [ Since, √3 = 31/2.] Now equating the powers, we get  x - 3 = (x + 2)/2 or, 2x - 6 = x + 2  Find  .....

Here,  4x - 1 = (√2)x or, 22(x - 1) = 2x/2             [Since, √2 = 21/2.] Comparing the exponents, we get  2x - 2 = x/2 or, 4x - 4 = x Complete .....

Here,      3x + 1 - 3x = 54 or, 3x . 31 - 3x = 54     [ Since, xm + n .....

Here,  103y - 3 = 1/0.001 or, 103y -3 = 103 or, 3y - 3 = 3 Now solve for y, you will get, y =  .....

Here,        32x+1 = 92x-1 or, 32x + 1 = 32(2x - 1) or, 2x + 1 = 2(2x - 1) or, 2x + 1 = 4x - 2 or, 2x = 3 or, x = 3/2. Thus, x = 3/2 is the required .....

Here,      42x - 1 = 2x+1 or, 22(2x - 1) = 2x + 1 Equating the exponents, we get or, 2(2x - 1) = x + 1  or, 4x - 2 = x + 1 or, 3x = 3 or, x = 3/3 = 1 .....

Here,      9x - 1 = 3x + 1 or, 32(x - 1) = 3x + 1 Equating the exponents, we get      2(x - 1) = x + 1 or, 2x - 2 = x + 1 or, 3x = 3 or, x = 3/3 = 1 .....

.....

In the second step, we can write  = (x1/a / x1/b)ab ⨯  (x1/b / x1/c)bc ⨯ (x1/c / x1/a)ca   [ Since, n√xm = xm/n.] =  (x1/a -1/b)ab ⨯ (x1/b -1/c)bc ⨯(x1/c .....

.....

.....

Here,  In second step, given question can be written as, = x(a2 - b2)/(a+b).x(b2 -c2)/(b+c).x(c2 - a2)/(c+a).   [ Since, n√xm = xm/n.] = x(a+b)(a-b)/(a + b).x(b +c)(b -c)/ (b + c).x(c+ a)(c-a)/(c+a)    .....

Here, ax.ayx-yazayy+z×azaxz+x    = (ax + y)x - y .  ( az - y )y + z .( az - x )z + x    [ Since, xm.xn = xm + n & xm/ xn = xm - .....

.....

.....

xbxc1bc× xcxa1ac×xaxb1ab  = xb-cbc×xc-aac×xa-bab  [ using law of indices] = xbbc-cbc×xcac-aac×xaab-bab = x1c-1b×x1a-1c×x1b-1a = x1c-1b+1a-1c+1b-1a = x0  = .....

.....

xa2+b2x-aba-b× xb2+bcx-c2b-c×xc2+acx-a2c-a = xa2+ab+b2a-b×xb2+bc+c2b-c×xc2+ca+a2c-a [using law of indices]   =xa3-b3 × xb3-c3×xc3-a3 [using formula a3-b3] = .....

ax+y2ay+z2az+x2ax.ay.az4 = a2x+2y  × a2y+2z× a2z+2x a4x .a4y.a4z = a2x+2y+2y+2z+2z+2x   a4x+4y+4z =  a4x+4y+4z  a4x+4y+4z .....

xa÷xba2+ab+b2×xb÷xcb2+bc+c2× xc÷xac2+ca+a2 = xa-ba2+ab+b2×xb-cb2+bc+c2×xc-ac2+ca+a2 [using law of indices] = xa3-b3 × xb3-c3×xc3-a3  [using formula of a3-b3] = .....

xax-ba-b× xbx-cb-c×xcxac+a =x(a+b)(a-b) ⨉ x(b+c) (b-c) ⨉ x(c-a) (c+a)    =xa2-b2×xb2-c2×xc2-a2   [using formula :a2-b2= (a+b)(a-b)] = .....

Here,  xa+bxca - b  ×xc+axbc-a×xb+cxab-c =   xa2-b2xca-cb×xc2-a2xbc-ab×xb2-c2xab-ac =   xa2-b2+c2-a2+b2-c2xca-cb+bc-ab+ab-ac = x0 / x0 = 1/1 = .....

= x+yx-y-x-yx+y-4xyx+yx-y = x+y2- {x-y2}x+yx-y-4xyx+yx-y  (taking LCM) = x2+2xy+y2- x2-2xy+y2x+yx-y-4xyx+yx-y = x2+2xy+y2-x2+2xy-y2 x+yx-y-4xyx+yx-y = 4xy x+yx-y-4xyx+yx-y = 4xy-4xyx+yx-y = 0x+yx-y = .....

There are three different levels of the executive in Nepal in federalism. They are federal (central), provincial and local level executive. The provincial executive carries out the following functions: - It has the power to run the matter of the .....

The cavity in between those two membranes is filled with a fluid called as pericardial fluid. It protects the heart from shock and injuries. Also, it allows the frictionless movement of the heart. The fluid in the brain and spinal cord that .....

They should also be regularly asked to schedule the cleanliness programme. Any person can be hired for sweeping the city or main street areas. Plantation or replantation can be done in any public areas. In this way, we can keep our surroundings .....

iv. Organizing frequent interactions and meeting among students, their guardians, teachers and local social workers to raise awareness against brain drain. v.  Diversifying the markets so that different sectors can be established for the .....

Mostly, mother accompanies her children. There is a saying “Mother’s heart is as wide as the horizon and as deep as the ocean for a child.” She can teach her children about the good manner and life skills. The children getting a .....

A hyperlink is an element in an HTML document that links to either another portion of the document or to another document .....

Practice as noun and  Practise as a verb.  See the example.  a. I have a practice book.  b. I have to practise important questions. Practising this helps you grab good .....

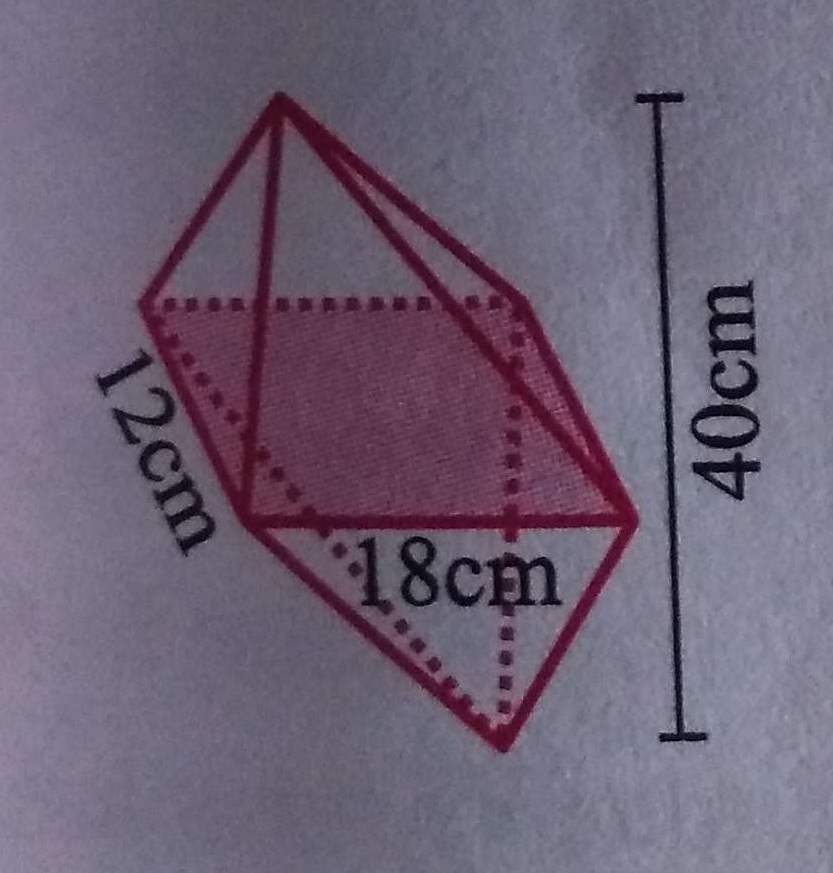
Surface area is a two-dimensional property of a three-dimensional figure. When solids are joined together, such as a hemisphere on a cone, the surface area of the connecting circle is not included in the overall surface area - it is .....

Here,  Let h be the height of upper pyramid and H be the fight of lower pyramid. Then,  Total height = h + H = 40cm. Now,  Volume of solid = Volume of  uppre pytamid + Volume of lower pyramid        .....

Here,  ao , 2ao , 4ao and 5ao are the angles of a quadrilateral. So,      ao .....

Here,  x0, 3x0, (x0 + 150) and (2x0 + 300) are the angles of a quadrilateral So,     xo +  3xo+ (xo + 15o) +  (2xo + 30o) = 360o   [ ∵ the sum of .....

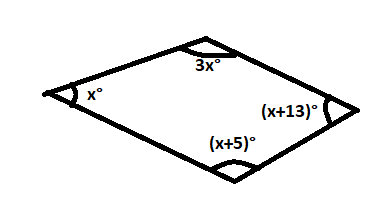
Here, x+3x+(x+13)+(x+5) = 360o [ sum of angles of quadrilaterals ] or,6x+18= 360o or, 6x=342o  or x= 342o/6 So,x= .....

We have given, A+B=60° Operating both sides by cos, or, cos(A+B)=1/2 or, cosA.cosB−sinA.sinB=1/2     [ Since, using formula of cos(A+B).] or, 2cosA.cosB−1=2sinA.sinB squaring both sides, or, .....

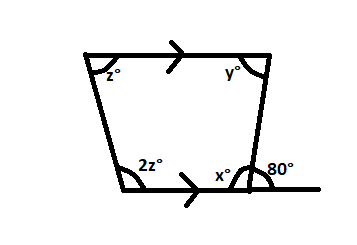
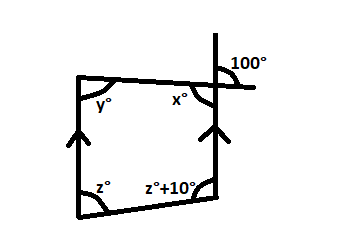
Here, y=80o [ Being alternate angle] x+80o = 180o [ being linear pair] or,x=180o - 80o or,x=100o  Now, z+2z+x+y=360o [ Sum of angles of quadrilateral] Now, put the values of x and y from above and calculate to find .....

Here, x=100o [ Being vertically opposite angles] x+y=180o [ Sum of co-interior angle] or,100o + y = 180o ( putting value of x)  or,y =80o Now, y+x+z+z+10o = 360o [ sum of angles of quadrilaeral] From here, put .....

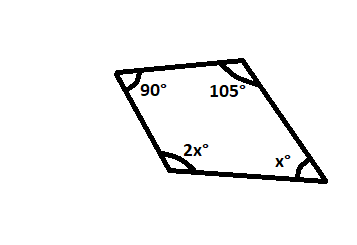
Here,  2x+x+90o+105o  = 360o  [ sum of angles of quadrilateral is 360o ] or,3x+ 195o  = 360o or,3x= 360o - 195o  or, x= .....

Here, y+ 2y+ 80o +145o = 360o [  sum of angles of quadrilateral ] or, 3y+ 225o = 360o or, 3y = 360o - 225o Now, calculate and find the value of .....

Here, x + 65o + 115o + 130o  =  360o [ Sum of angles of quadrilateral is 360o] or, x+ 310o = 360o So, x= .....

Here, x2 - 2x + 1 - y2 = x2 - 2.x.1 + 12 - y2 = (x - 1)2 - y2                 [ Since, a2 -2ab + b2 = (a + b)2.] Now use the .....

x4 + x2y2 + y4 =  x4 + x2y2 + y4 = [(x2)2 + 2x2y2 + (y2)2] - x2y2        (one term x2y2is added and subtracted)  = (x2 + y2)2 – (xy)2,                  .....